题目内容

输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。

输入格式

第一行包含三个整数n，m，q。
接下来n行，每行包含m个整数，表示整数矩阵。
接下来q行，每行包含四个整数x1, y1, x2, y2，表示一组询问。

输出格式

共q行，每行输出一个询问的结果。

数据范围

1≤n,m≤1000 ,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000

输入样例

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例

17
27
21

题解

通过一个图和两个公式来说明。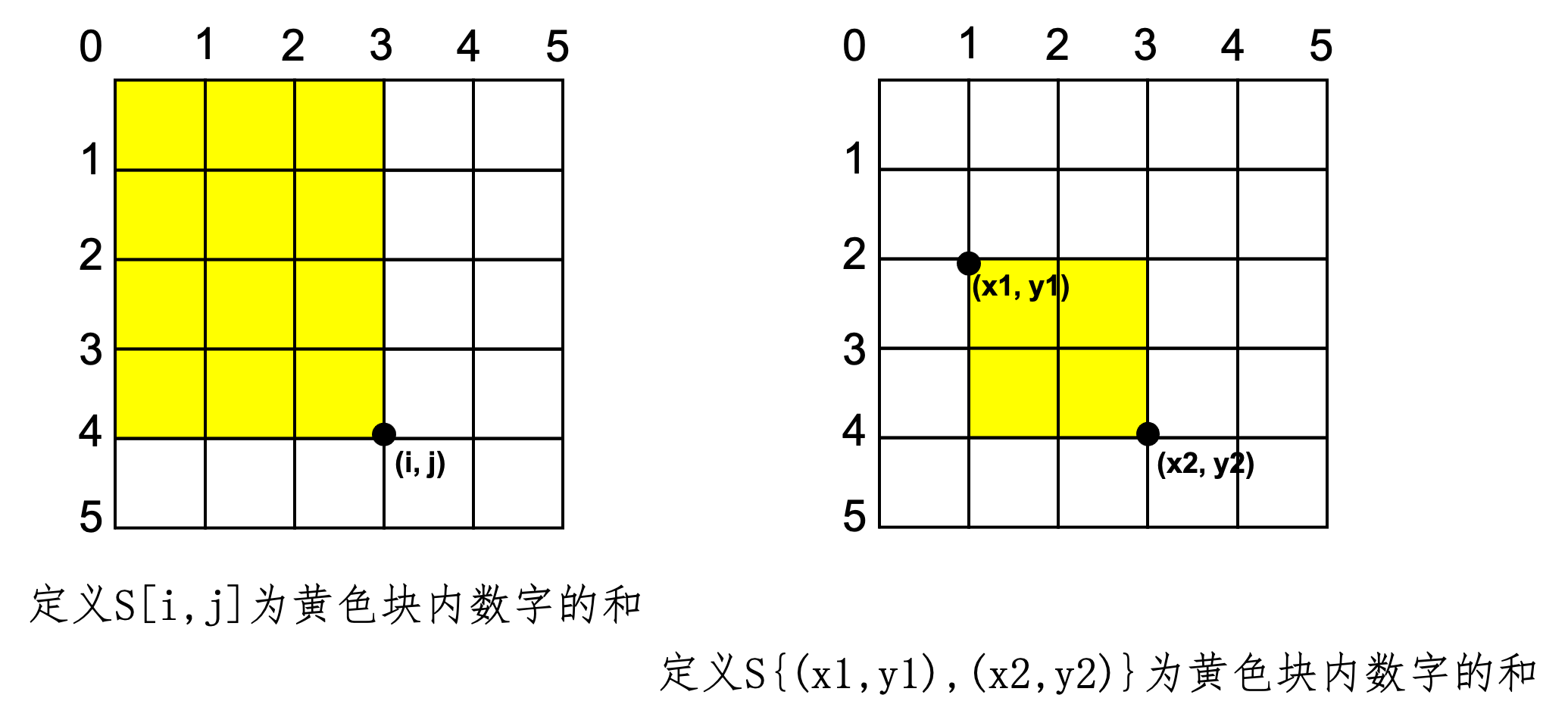

S[i, j] = S[i - 1, j] + S[i, j - 1] - S[i - 1, j - 1] + a[i, j]
S{(x1,y1),(x2,y2)} = S[x2, y2] - S[X1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

代码

#include <iostream>

using namespace std;

const int N = 1010;

int a[N][N],s[N][N];
int n,m,q;

int main(){
    scanf("%d%d%d",&n,&m,&q);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            scanf("%d", &a[i][j]);
    //初始化前缀和数组
    for (int i = 1;i <= n; i++)
        for (int j = 1; j <= m; j++)
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
    //询问
    while (q--){
        int x1,y1,x2,y2;
        scanf("%d%d%d%d", &x1,&y1,&x2,&y2);
        printf("%d\n",s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]);
    }
    return 0;
}