题目内容
给你 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器。
示例
示例 1: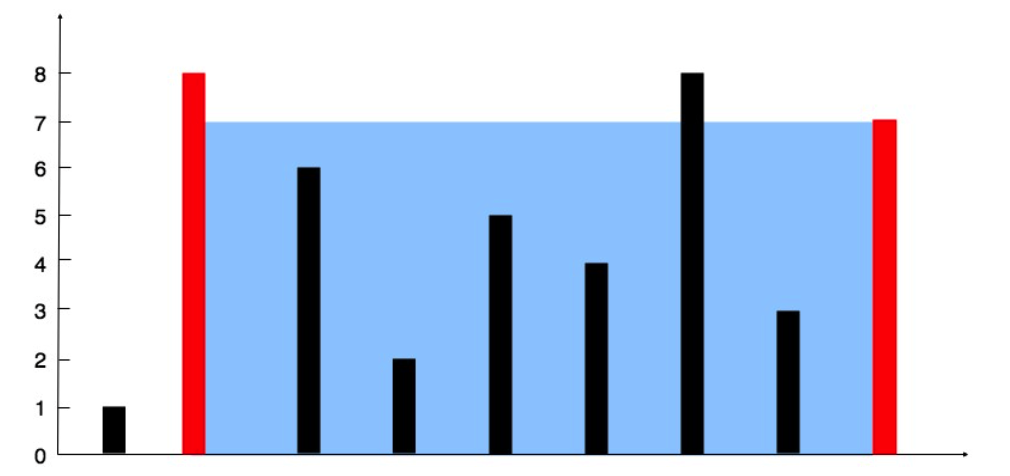
输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
示例 3:
输入:height = [4,3,2,1,4]
输出:16
示例 4:
输入:height = [1,2,1]
输出:2
提示
n = height.length
2 <= n <= 3 10^4
0 <= height[i] <= 3 10^4
题解
本题又是一道有关指针扫描的问题,思路如下:
将两个指针分别指向左端点和右端点,然后求面积;接着比较两个指针代表的边界高度,哪个小就往前移动,继续求面积,最后得出最大的面积。
这里需要证明上述方法是能得到最优解的方法:
假设最优解对应的两条线的下标是 i′,j′(i′<j′),在 i,j 不断靠近的过程中,不妨假设 i 先走到 i′,则此时有 j′<j。反证,如果此时 ai ≤ aj,设 S 表示 i,j能盛多少水,S′ 表示 i′,j′能盛多少水,则:
S=min(ai,aj)∗(j−i)
=ai∗(j−i)
ai∗(j′−i)
≥min(ai,aj′)∗(j′−i)=S′
与 S′是最优解矛盾,因此 ai>aj,所以 j 会一直走到 j′,从而得到最优解。
代码
class Solution { |

