题目内容

实现 strStr() 函数。

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回 -1 。

说明：

当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。

对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与 C 语言的 strstr() 以及 Java 的 indexOf() 定义相符。

示例

示例 1：

输入：haystack = “hello”, needle = “ll”
输出：2

示例 2：

输入：haystack = “aaaaa”, needle = “bba”
输出：-1

示例 3：

输入：haystack = “”, needle = “”
输出：0

提示

0 <= haystack.length, needle.length <= 5 * 10^4
haystack 和 needle 仅由小写英文字符组成

题解

本题有两种求解的方式，第一种是暴力求解，第二种为KMP算法（Knuth-Morris-Pratt字符串查找算法）的应用。

我将原题中的haystack数组名改为了s，needle改为了p，这样写代码比较方便简单，以下用s和p代替。

第一种暴力求解算法实现很简单，即为两重循环，外层循环s，内层循环p，找出匹配过程中的最大长度即可。这个思路很容易理解，也是所有人都能想到的，但是时间复杂度为O(nm)，有些大，如果题目中给出的数据范围过大，可能会出现超时的情况。

第二种为KMP算法，时间复杂度为O(n+m)。

首先，KMP算法一般将字符串下标调整为1开始比较好处理，所以，可以将题目中给出的下标前面添加空字符或者其他任意字符，让s和p的真正字符串起始下标+1。

接下来，按照如下操作步骤操作即可得出结论：

1、定义一个next数组，记为next[j]，意思是所有p[1-j]中非平凡（不包括p这个字符串本身）的相等的前缀与后缀的长度的最大值记录一个next[j]。这里的前缀和后缀表示：从下标1开始的前缀和以j为结尾的后缀。

2、在构造出next数组后，找出一个最大值即为答案。

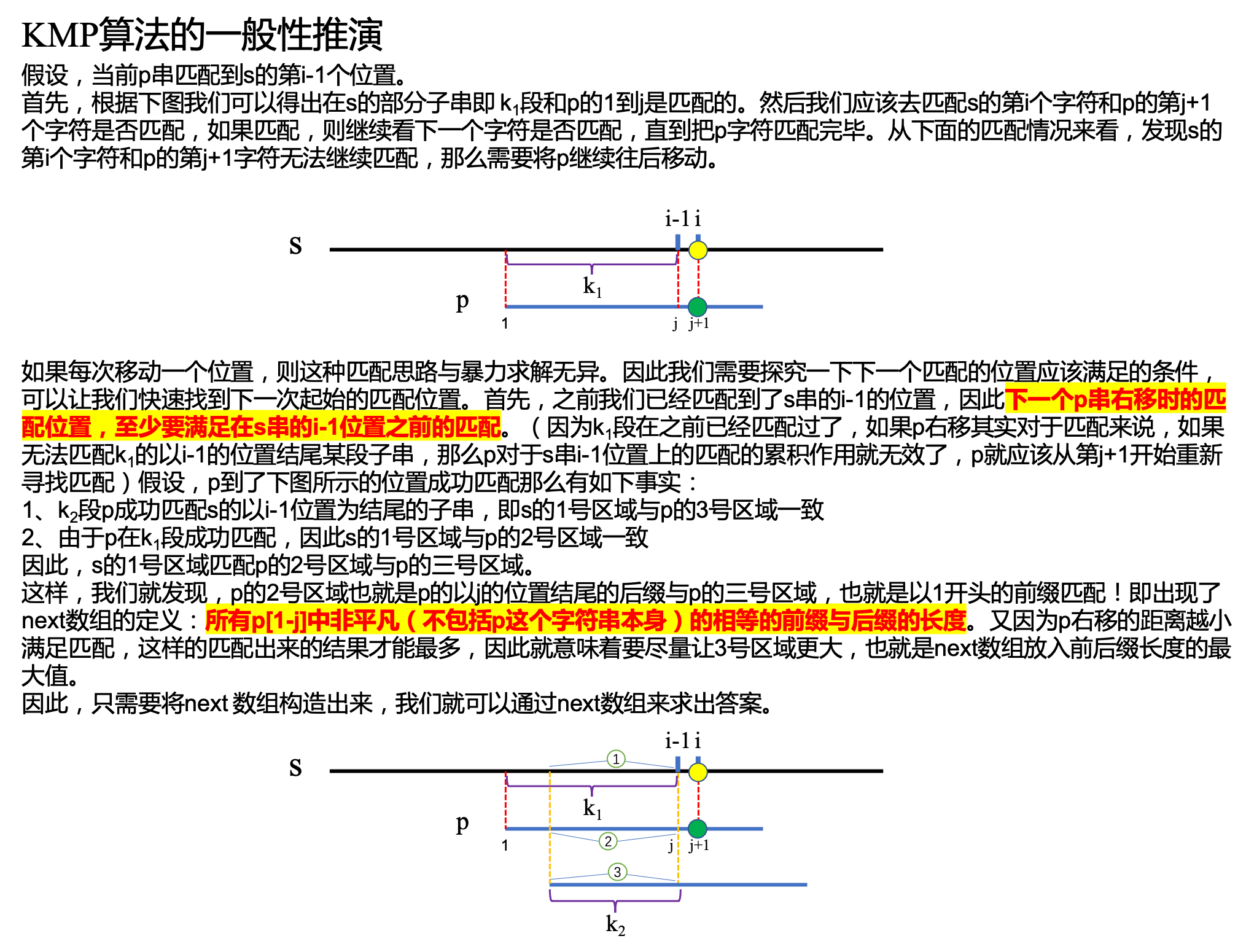
这里做一个一般性的推演，来辅助理解next数组对求解的意义。

代码

class Solution {
public:
  	//int strStr(string s, string needle) {
    int strStr(string s, string p) {
        //KMP算法。一般习惯下标为1开始比较好处理。
        //next[i]:所有p[1-i]中的相等的前缀和后缀的长度的最大值
        if(p.empty()) return 0;

        int n = s.size(), m = p.size();
        s = ' ' + s, p = ' ' + p;//将字符串长度+1

        vector<int> next(m + 1);//定义一个next数组，且长度为m+1，因为p字符串的长度增加了1.

        //求的时候i从2开始，因为next[1]=0.（始终记住，真正字符串的下标从1开始，所以next[1]=0）
        //本循环是求next数组的过程，因此也就是要找到p的每个位置上的对应前缀和后缀的最大值，因此分析过程与上图推演的类似，只是把s串换为p即可。
        for(int i = 2, j = 0; i <= m; i++){
          	//当j不为0时且p的第i位与p的j+1不匹配时，j就更新为next[j]。因为next[j]就是以j位置的下一次的最大匹配的位置，也就是满足p的前缀后缀相等的最大长度的下一个匹配的j的坐标。
            while(j && p[i] != p[j+1]) j = next[j];
            if(p[i] == p[j+1]) j++;//说明匹配，j就往后移动继续匹配
            next[i] = j;//这里是找出了最大匹配的长度也就是j
        }

        //这里是s和p串的匹配过程
        for(int i = 1, j = 0; i<=n; i++){
            //当j不为0.且s的i位置与p的j+1位置不匹配，j进行更新。
            while(j && s[i] != p[j + 1]) j = next[j];
            //如果匹配，j++
            if(s[i] == p[j + 1]) j++;
            //当第一次匹配全部的p，返回当前的下标即(i-m+1)-1。这个括号后面的-1是因为开始我们将字符串本身的长度增加了1噢，所以要减掉。
            if(j == m) return i - m;
        }
        //如果没找到，则返回-1
        return -1;
    }
};