题目内容
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
进阶:你可以设计一个时间复杂度为 O(log n) 的解决方案吗?
示例
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
示例 3:
输入:nums = [1], target = 0
输出:-1
提示
1、1 <= nums.length <= 5000
2、-10^4 <= nums[i] <= 10^4
3、nums 中的每个值都 独一无二
4、题目数据保证 nums 在预先未知的某个下标上进行了旋转
5、-10^4 <= target <= 10^4
题解
本题在求解上也是采用二分的思想来做。可以先画个简图方便我们理解。
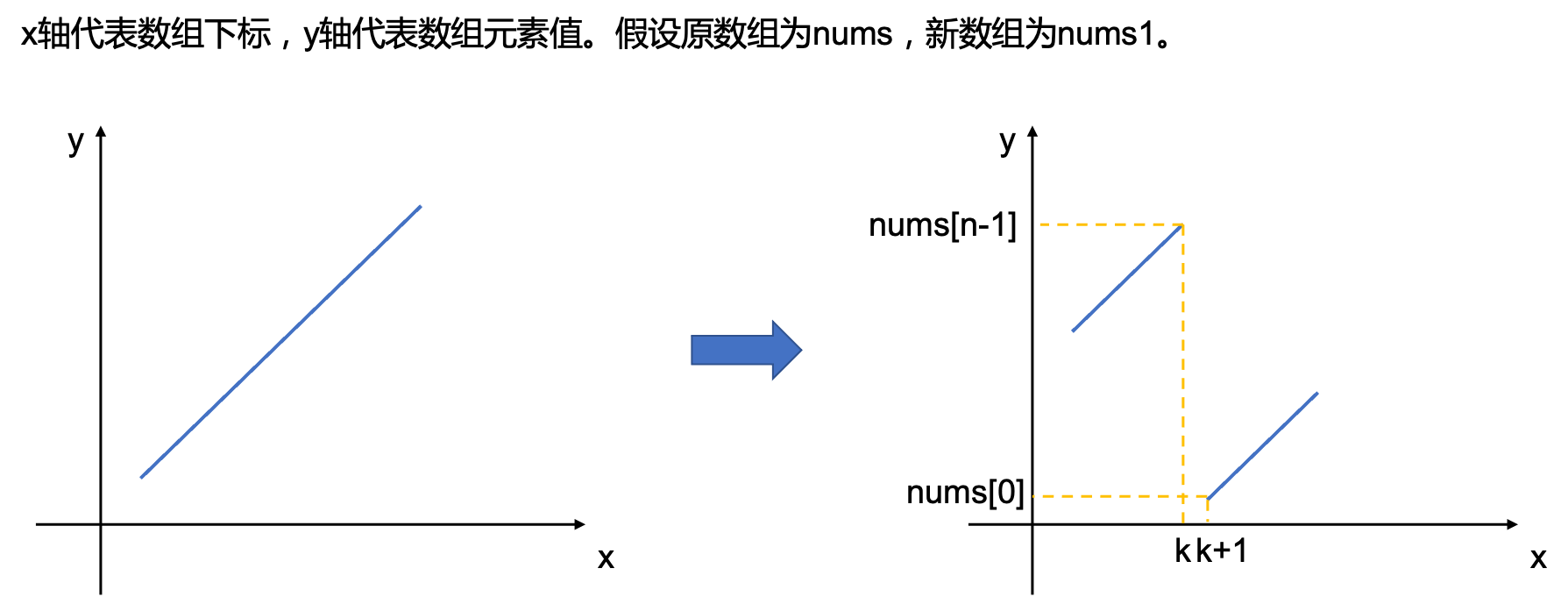
然后,我们根据图,开始思考本题的思路
1、二分的基本思想就是某个分界点将区间分为两段,一个区间内满足某种性质,一个区间不满足,找出满足区间的那一段并更新为下一次求解的区间,在该区间内继续寻找分界点,重复上述操作,直到区间被更新为一个点或者左边界大于右边界时停止。
2、在本题中,我们需要找到target的下标。因此,针对本题来说,首先要找到两个区间的分界点,也就是k的下标,将两个旋转的区间分开,也是同样采用二分的方式,去判断区间的值与nums[0]的大小关系,一段区间均大于等于,一段均小于。这个查找完了之后,二分的左右端点相等,等于k。
3、然后我们要判断target在哪一段区间内。直接判断target与nums[k]的关系,确定target属于的区间范围,然后更新二分算法的左右端点。
3、判断出target在哪个区间之后,由于之后的区间不需要考虑旋转的问题,所以继续使用普通的二分做就可以了。本题主要是第一次的二分,需要特殊判断一下即可。
接下来,请看代码以及注释。
代码
class Solution { |

