题目内容
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例
示例 1:
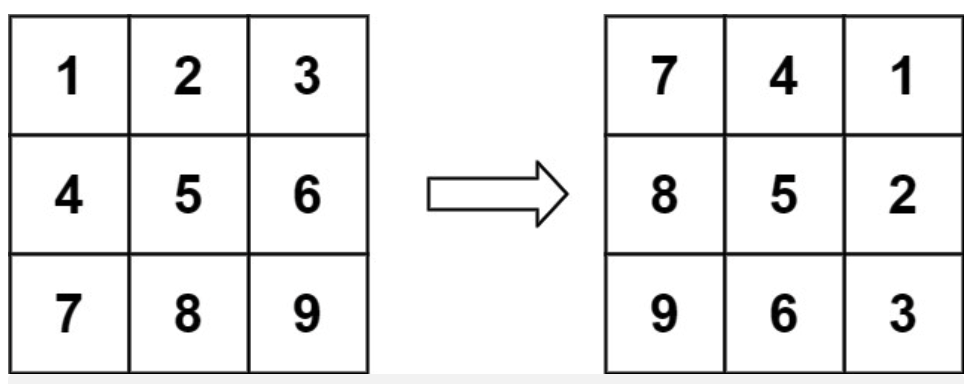
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:
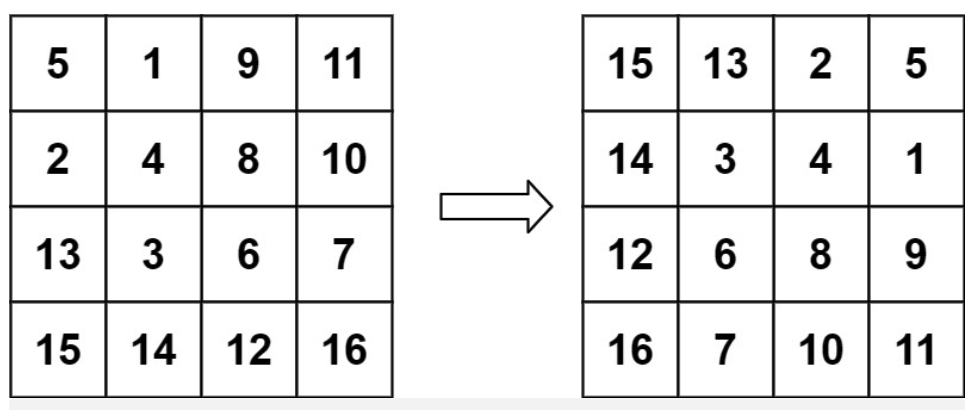
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
示例 3:
输入:matrix = [[1]]
输出:[[1]]
示例 4:
输入:matrix = [[1,2],[3,4]]
输出:[[3,1],[4,2]]
提示
matrix.length == n
matrix[i].length == n
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000
题解
本题是一道经典的旋转矩阵的题,直接思考旋转90°会比较困难。我们可以将此拆分成两个步骤进行求解,即
1、按照左上-右下对角线进行翻转
2、再按照中轴竖线进行对称翻转
矩阵经过上述变形后与旋转90°的结果一致。
由于每一类旋转均按照行或者列,n次,因此一共的事件复杂度是O(n^2),由于仅存在交换操作,因此每一次的交换操作需要存储一个临时变量,因此空间复杂度为O(1)。
具体,请看代码。
代码
class Solution { |

