题目内容
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
示例
示例 1:
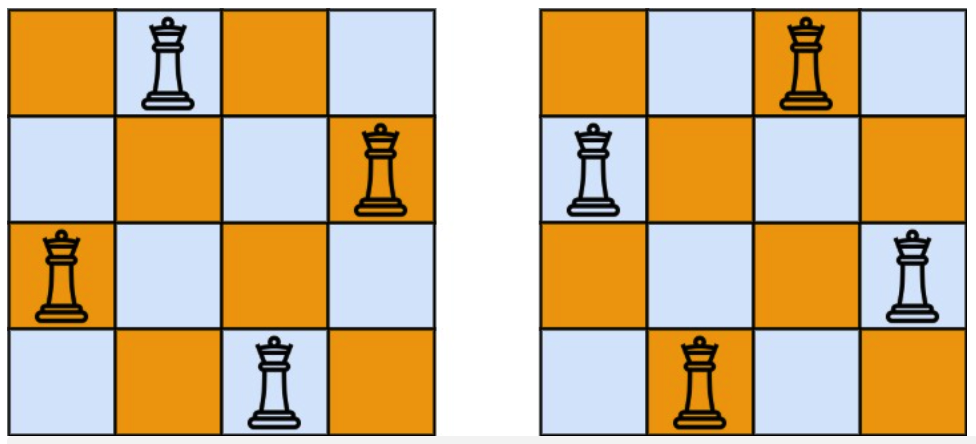
输入:n = 4
输出:[[“.Q..”,”…Q”,”Q…”,”..Q.”],[“..Q.”,”Q…”,”…Q”,”.Q..”]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[[“Q”]]
提示
1、1 <= n <= 9
2、皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
题解
本题是n皇后问题,主要思路还是深度优先搜索。
这里,我们定义一些布尔数组来存放当前格子是否存在皇后,用于n皇后的规则判断,定义 vector
使用dfs搜索时需要使用4个参数来记录状态,分别是:当前遍历格子横坐标、当前格子纵坐标、整体已摆放的皇后个数、棋盘大小。
对于每步搜索,有两种选择:
1、当前格子不放皇后,则转移到 dfs(x, y + 1, s, n);
2、如果 (x,y) 所在的行、列、对角线不存在皇后,则当前格子可以摆放皇后,更新row, col, dg,udg后转移到 dfs(x, y + 1, s + 1, n),回溯时不要忘记恢复row, col, dg, udg等状态。
时间复杂度分析:由于 n 个皇后不能在同行同列,所以每行恰有一个皇后,在不考虑对角线的情况下,方案数的上限:第一行有 n 个位置可选,第二行有 n−1 个位置可选,依次类推,可得方案数最多是 n!。所以时间复杂度是 O(n!)。
代码
class Solution { |

