题目内容

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

示例

示例 1：

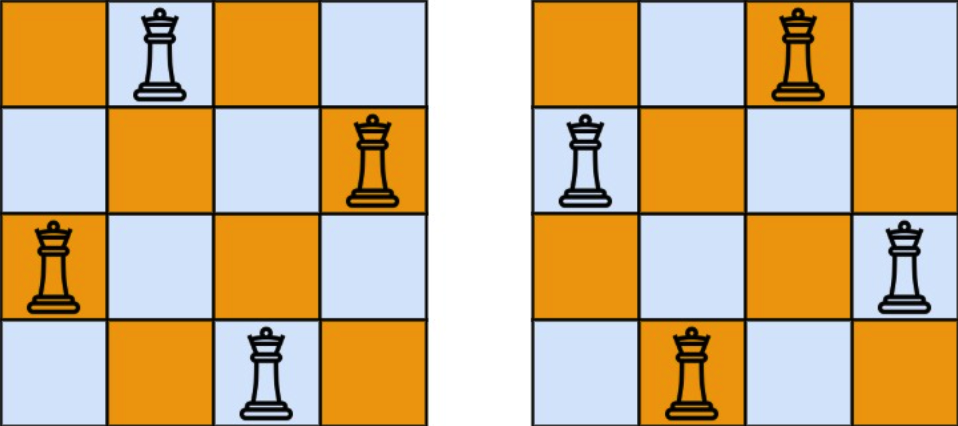
输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：1

提示

1、1 <= n <= 9
2、皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上

题解

本题与上题不同点在于本题求方案数，因此可以在搜索函数中直接累计求出。

在思路上，与上题完全一致，就是根据n皇后的规则进行判断，首先，用布尔数组表示出两条对角线的和以及行和列的放置情况。由于某列存在元素时，对应下标的行也一定有元素，因此我们仅需要定义一个行标志数组或者列标志数组就好了。

在对角线的表示问题上，可以通过表示截距来判断是否在同一对角线。如下图所示：

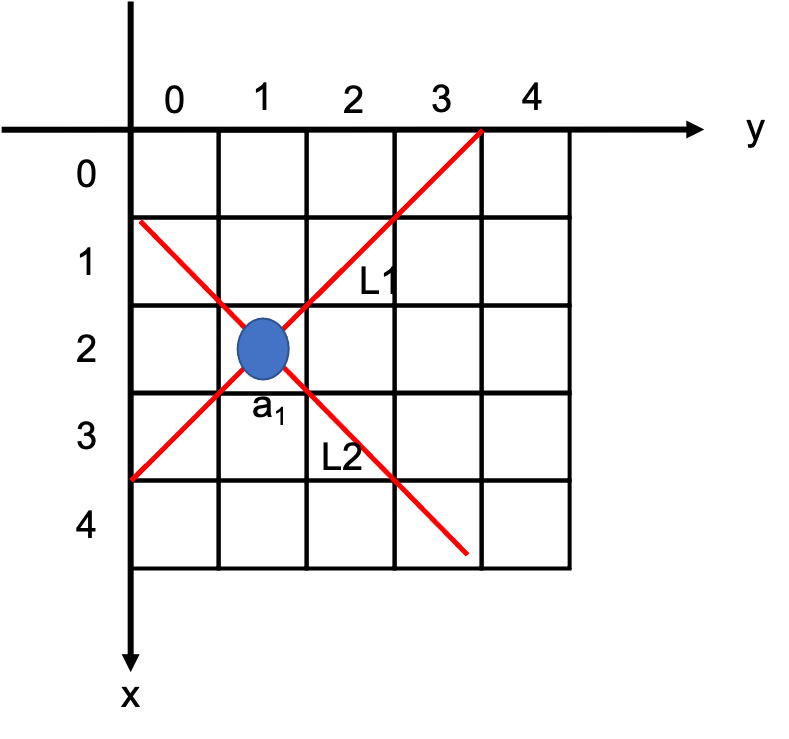
由于每个点都会代表两条对角线，因此我们需要思考一下如何映射对角线，在相同对角线上的点能够映射出来同一条对角线上即可。这里使用直线表达式的截距来进行表示。类似L1的对角线有9条，类似L2的对角线也有9条，即2n-1，我们初始化的时候直接初始化为2n即可。类似L1的表达式为 y = -x+k，类似L2的表达式为y = x+k。然后，为了保证我们创建的对角线截距数组的下标一致，又因为L2的截距是从-4到4，因此需要对其加上n，即y = x+k+n在本图中n为5，这样就保持其截距范围映射到了1到9，与L1的下标映射保持一致。

具体，请看代码。

代码

class Solution {
public:
    int n;
    vector<bool> col, dg, udg;

    int totalNQueens(int _n) {
        n = _n;
        col = vector<bool>(n);
        dg = udg = vector<bool>(2 * n);
        return dfs(0);//由于仅仅需要考虑方案数，因此不需要记录结果答案。
    }

    int dfs(int u) {
        if (u == n) return 1;//当遍历到了最后一行，则说明遍历完毕，就存在一种情况，所以返回1.
        int res = 0;
        for (int i = 0; i < n; i ++ ) {
            if (!col[i] && !dg[u - i + n] && !udg[u + i]) {
              	//这里进行判断对角线方案。
                col[i] = dg[u - i + n] = udg[u + i] = true;
                res += dfs(u + 1);
                col[i] = dg[u - i + n] = udg[u + i] = false;
            }
        }

        return res;
    }
};