题目内容

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例

示例 1：

输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。

​ 向右 -> 向下 -> 向下

​ 向下 -> 向下 -> 向右

​ 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示

1、1 <= m, n <= 100
2、题目数据保证答案小于等于 2 * 10^9

题解

本题是一道经典的DP问题，即动态规划的问题。

首先，机器人只能向右或者向下走，因此我们可以对一种情况进行简单地分析，从而得出结论，假设有3x4的矩阵，有如下情况：

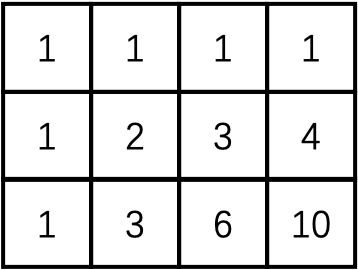
上述3x4的方格中，每个方格都表示到该方格的方案数。可以发现，每个方格的方案数都是由上一个方格和左边方格的方案数的加和。因此本题就可以将问题分成子问题看待，即最右下角的格子数由左边的格子和上方的格子的方案数确定，依此类推。

针对本题的DP问题，我们可以定义状态方程为F[i,j]，表示从(0,0)到(i,j)格子一共有多少种方案数。

然后思考一下递推方程：

1、当i和j均不为0时，F[i,j] = F[i-1,j] + F[i,j-1];

2、当i=0时，F[i,j] = F[i-1,j];

3、当j=0时，F[i,j] = F[i,j-1];

4、F[0,0] = 1。

具体，请见代码。

代码

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> f(n, vector<int>(m));//状态数组
        for (int i = 0; i < n; i ++ )
            for (int j = 0; j < m; j ++ )
                if (!i && !j) f[i][j] = 1;//i和j均为0的情况下，在起点，为1
                else {
                    if (i) f[i][j] += f[i - 1][j];//如果i大于0，说明可以从上方下来
                    if (j) f[i][j] += f[i][j - 1];//如果j大于0，说明可以用左边过来
                }
        return f[n - 1][m - 1];
    }
};