题目内容

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例

示例 1：

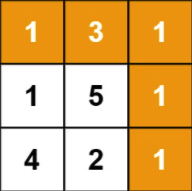
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示

1、m == grid.length
2、n == grid[i].length
3、1 <= m, n <= 200
4、0 <= grid[i][j] <= 100

题解

本题采用动态规划的思路求解。

首先，需要定义状态函数F[i][j]，表示从起点走到（i，j）点的所有路径和的最小值。

然后，我们来将此问题划分为子问题求解：因为最后一步是由前一步从下走或从右走得出来的，因此可以生成递推公式，如下：

前一个格子向下走：A = F[i-1][j] + grid(i,j)

前一个格子向右走：B = F[i][j-1] + grid(i,j)

那么，F[i][j] = min (A,B)

代码

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        //f[i][j]表示从起点走到(i,j)的所有路径和的最小值
        int n = grid.size();//首先，求解一下行数
        if(!n) return 0;//行数是0的话，直接返回0
        int m = grid[0].size();//前面条件满足后再求列数
        
        vector<vector<int>> f(n,vector<int>(m,INT_MAX));//状态表示方程，同时初始化值为INT的最大值
        for(int i = 0; i < n; i++)
            for(int j = 0; j < m; j++)
                if(!i && !j) f[i][j] = grid[i][j];//当处于起点时的情况
                else{
                  	//一般情况时
                    if(i) f[i][j] = min(f[i - 1][j] + grid[i][j], f[i][j]);
                    if(j) f[i][j] = min(f[i][j - 1]  +grid[i][j], f[i][j]);
                }
        return f[n - 1][m - 1];
    }
};