题目内容

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

进阶：想出一个仅使用常量空间的解决方案

示例

示例 1：

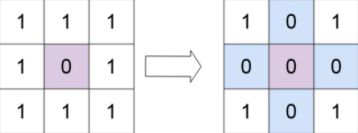
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

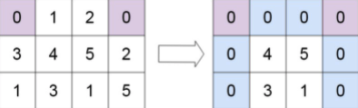
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示

1、m == matrix.length
2、n == matrix[0].length
3、1 <= m, n <= 200
4、-2^31 <= matrix[i][j] <= 2^31 - 1

题解

本题直接给出进阶的思路：

首先，根据题意，我们需要一个行数组和列数组来记录某行某列是否需要置零，请看下图：

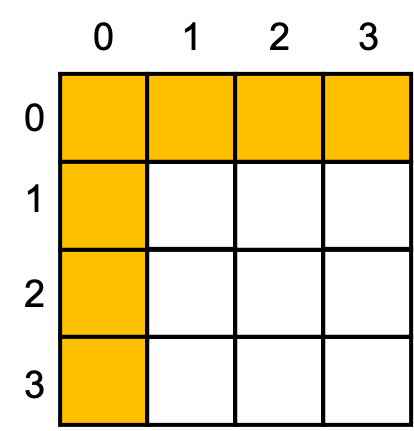
我们可以利用矩阵中的第0行和第0列用于记录矩阵的行、列是否置零的信息。如果某行需要置零，则对应第0列的对应位置一定需要置零，如果不需要，则对应位置保持原数即可。

具体做法上，如下：

1、首先，开两个临时变量，用于标记第0行和第0列本身是否存在0，因为如果存在0，直接就会将第0行和第0列全部置零，这样就无法使用这两个数组记录置零信息了，这个操作需要在全部操作完毕后再根据临时变量结果做出对应操作

2、然后遍历除第0行和第0列之外的全部元素，判断是否存在0；若存在，则将对应第0行或者第0列位置上的数置为0；若不存在，则继续寻找。

3、遍历第0行，将对应列置零

4、遍历第0列，将对应行置零

5、根据临时变量情况，将对应的第0行和第0列置零。

具体看代码。

代码

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        //这个题可以转换一下思路，就是说某个位置的行或者列中存在0，则需要换为0，如果某个位置的行或者列没有0，则不需要换为0。但是由于在修改的过程中，行列修改会造成整个原数组通过上述办法全部变为0，因此要用一个方法避免这种情况的发生。
        //可以用原数组第一行和第一列来记录其包含的方块中的情况，然后再开两个临时变量存储第一行和第一列是否存在0即可。
        if(matrix.empty() || matrix[0].empty()) return;
        int n = matrix.size(), m = matrix[0].size();
        int r0 = 1, c0 = 1;//初始化以下第一行和第一列的状态,1表示没有，0表示有。 
        for(int i = 0; i < m; i++) if(!matrix[0][i]) r0 = 0;//第一行，看看有没有0
        for(int i = 0; i < n; i++) if(!matrix[i][0]) c0 = 0;//第一列，看看有没有0

        for(int i = 1; i < m; i++)
            for(int j = 0; j < n; j++)
                if(!matrix[j][i])
                    matrix[0][i] = 0;
        
        for(int i = 1; i < n; i++)
            for(int j = 0; j < m; j++)
                if(!matrix[i][j])
                    matrix[i][0] = 0 ;


        for(int i = 1; i < m; i++)
            if(!matrix[0][i])
                for(int j = 0; j < n; j++)
                    matrix[j][i] = 0;
        
        for(int i = 1; i < n; i++)
            if(!matrix[i][0])
                for(int j = 0; j < m; j++)
                    matrix[i][j] = 0;
        
        if(!r0) for(int i = 0; i < m; i++) matrix[0][i] = 0;
        if(!c0) for(int i = 0; i < n; i++) matrix[i][0] = 0;

    }
};