题目内容

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

1、每行中的整数从左到右按升序排列。
2、每行的第一个整数大于前一行的最后一个整数。

示例

示例 1：

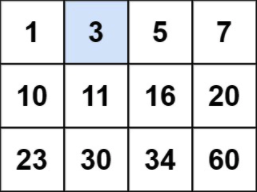
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

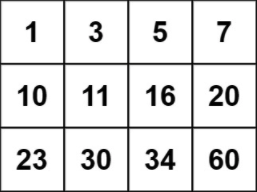
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

提示

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-10^4 <= matrix[i][j], target <= 10^4

题解

本题考查二分思想。由于矩阵每行和每列均势有序且单增，因此可以采用二分的方法。

在做法上，我们可以将这个矩阵看成按行来展开的一维数组，所以，我们需要将想象中的一维数组坐标转化为二维数组的下标即可。下面说明一下一维到二维坐标的转换：

前提定义：n为矩阵行数，m为矩阵列数。t为我们将二维数组展开后，每次二分的分界点的坐标，因此t的范围在0到nm-1。

转换操作：对应的二维数组的坐标为：（t/m,t%m）。由于m表示矩阵一行有多少个数，因此t/m就代表t中存了多少行，对应地就是t在二维矩阵中的行数。t%m就代表t在一行中的第几个位置，对应地就是t在二维矩阵中的列数。

代码

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        if(matrix.empty() || matrix[0].empty()) return false;
        int n = matrix.size(), m = matrix[0].size();

        int l = 0, r = n * m - 1; //二分
        while(l < r){
            int mid = l + r >> 1;
            if(matrix[mid / m][mid % m] >= target) r = mid;
            else l = mid + 1;
        }
        return matrix[r / m][r % m] == target;
    }
};