题目内容

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例

示例 1：

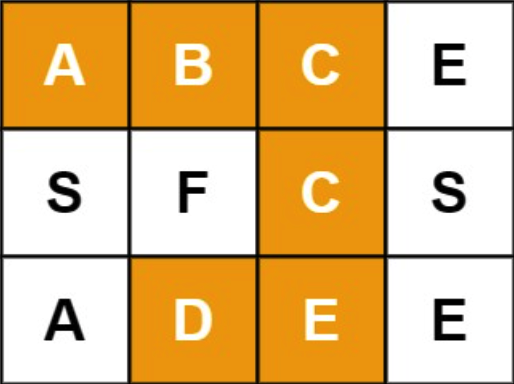
输入：board = [[“A”,”B”,”C”,”E”],[“S”,”F”,”C”,”S”],[“A”,”D”,”E”,”E”]], word = “ABCCED”
输出：true

示例 2：

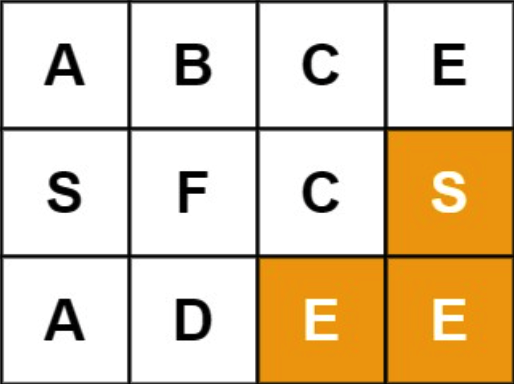
输入：board = [[“A”,”B”,”C”,”E”],[“S”,”F”,”C”,”S”],[“A”,”D”,”E”,”E”]], word = “SEE”
输出：true

示例 3：

输入：board = [[“A”,”B”,”C”,”E”],[“S”,”F”,”C”,”S”],[“A”,”D”,”E”,”E”]], word = “ABCB”
输出：false

提示

1、m == board.length
2、n = board[i].length
3、1 <= m, n <= 6
4、1 <= word.length <= 15
5、board 和 word 仅由大小写英文字母组成

题解

本题考查深度优先搜索。在具体思路上，需要首先把起点确定，然后再根据4个方向继续搜索即可。不过需要注意的是，从起点往后的所有点仅需要枚举三个方向，因为题目中说明单元格内的字符不能重复使用。

在dfs函数参数的思考上，首先，需要有传入的board的参数，然后有当前已经搜索到的路径的参数word，还应该有当前搜索到第几个数u这个参数，最后是需要搜索的单元格坐标x和y。

这里需要说明的是，我们为了防止一次搜索的过程中出现重复搜索单元格的情况，针对每一次的深度优先搜索的路径，搜索过一个单元格之后，将其值改为’.’，用于标识已经搜索过。记得还原现场即可。

时间复杂度分析：首先，起点枚举有$n^2$个，然后对于每个起点一共有$3^k$个不同的路径，k代表平均路径长度。所以为O
($n^23^k$)

代码

class Solution {
public:
    bool exist(vector<vector<char>>& board, string word) {
        //枚举起点，然后再枚举4个方向进行搜索。
        for(int i = 0; i < board.size(); i++)
            for(int j = 0; j < board[i].size(); j++){
                if(dfs(board, word, 0, i, j)) return true;
            }
        return false;
    }
    int dx[4] = {-1,0,1,0}, dy[4] = {0,1,0,-1};

    bool dfs(vector<vector<char>>& board, string& word, int u, int x, int y){
        //u表示当前搜到第几个位置，x、y代表当前点的坐标
        if(board[x][y] != word[u]) return false;//当前的位置上的字母不等于word的对应字母，返回false
        if(u == word.size() - 1) return true;//搜索完毕 返回true

        char t = board[x][y];
        int n = board.size(), m = board[0].size();
        board[x][y] = '.';//表示该字符已经被用过，标记一下。
        for(int i = 0; i < 4; i++){
            int a = x + dx[i], b = y + dy[i];
            if(a < 0 || a >= n || b < 0 || b >= m || board[a][b] == '.') continue;
            if(dfs(board,word,u+1,a,b)) return true;
        }   
        board[x][y] = t;//还原现场
        return false;
    }
    
    
};