题目内容
给你二叉搜索树的根节点 root ,该树中的两个节点被错误地交换。请在不改变其结构的情况下,恢复这棵树。
进阶:使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用常数空间的解决方案吗?
示例
示例 1:
输入:root = [1,3,null,null,2]
输出:[3,1,null,null,2]
解释:3 不能是 1 左孩子,因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。
示例 2:
输入:root = [3,1,4,null,null,2]
输出:[2,1,4,null,null,3]
解释:2 不能在 3 的右子树中,因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。
提示
1、树上节点的数目在范围 [2, 1000] 内
2、-2^31 <= Node.val <= 2^31 - 1
题解
本题在求解的时候,如果没有题目中的进阶O(1)的限制,我们可以通过寻找中序遍历中的逆序对。因为是两个点被交换,那么一定存在两个逆序对,假设为A和B,则只需要将A中的大值和B中的小值交换即可。比如:原来为12345678,将2和6交换后,变成了16345278。逆序对为63和52,因此交换63的6以及52的2即可。
但是本题要求O(1)的空间复杂度,因此我们需要采用一个叫做Morris算法来求解。
大概讲一下Morris算法。
首先,从根节点开始遍历,直到当前节点为空为止:
1、如果当前节点没有左儿子,打印当前点的值,进入其右儿子
2、如果当前节点有左儿子,则需要找该节点的前驱
(1)如果前驱节点的右儿子为空,说明左子树没有被遍历过,进入左子树遍历,并将前驱节点的右儿子修改为当前节点,方便找到该节点进行回溯。
p->right == NULL, p->right = root, root = root->right
(2)如果前驱结点的右儿子为当前节点,则说明左子树已经被遍历过,则将前驱结点的右儿子恢复为空,然后打印当前节点的值,进入右儿子继续遍历。
p->right = NULL,; 遍历root;root = root->right
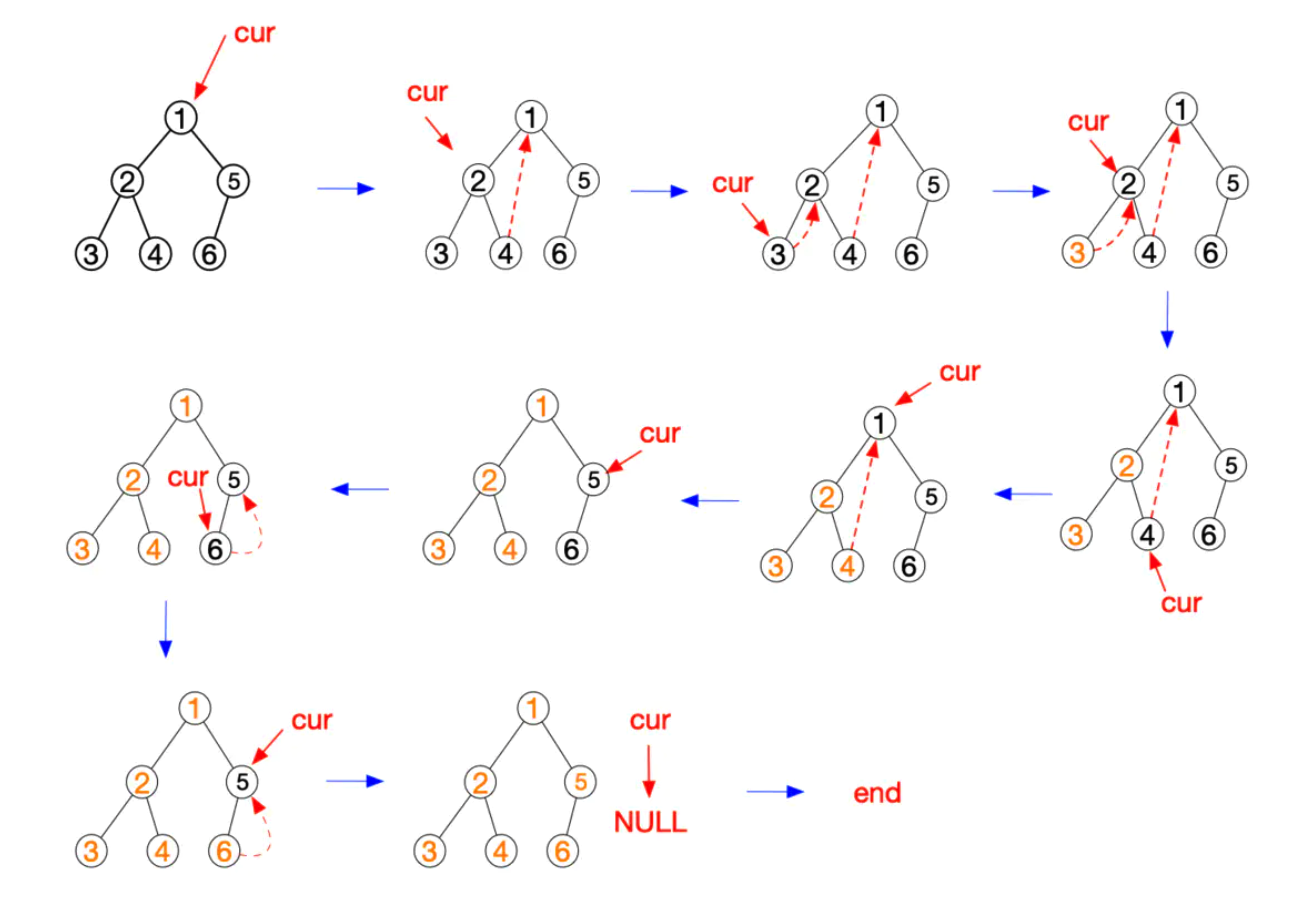
这里额外的空间就是存储了每颗左子树的遍历的最后一个点的右儿子为当前节点。(这里注意,最后一个点必定没有右儿子!)
代码
/** |

