题目内容

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

请优化你的算法到 O(rowIndex) 空间复杂度。

示例

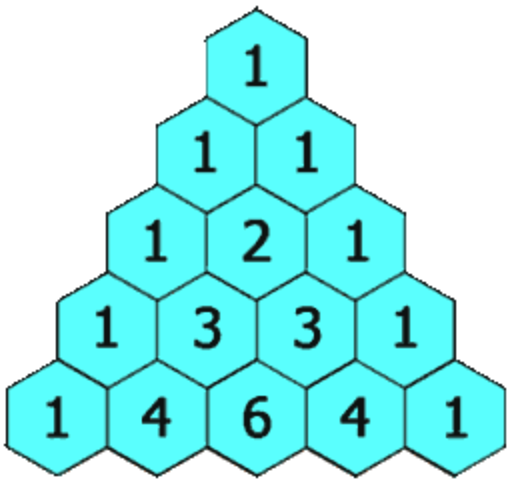
示例 1:

输入: rowIndex = 3
输出: [1,3,3,1]

示例 2:

输入: rowIndex = 0
输出: [1]

示例 3:

输入: rowIndex = 1
输出: [1,1]

提示

0 <= rowIndex <= 33

题解

有两种解法。

第一种，找规律。对于杨辉三角，每一行元素都是(x+1)^2的展开式的对应系数，因此从第0行开始计算，对于第k行，有k+1个元素，分别对应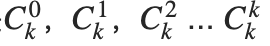.根据公式，求其答案。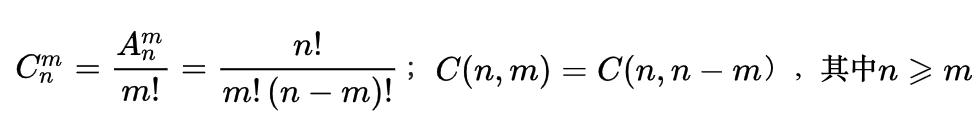

第二种，递推法。使用滚动数组求解，一行一行的计算。每一行仅与上一行的值有关，因此在计算每一行的值的时候，可以先将1放在首和尾两个位置，然后计算中间的数。

滚动数组:有A和B两行的数组，通过递推，能够重复利用相互行的值进行计算。举个例子：A行的值能推出B行的值，然后根据B行的值可以推出下一行的值，但A行的值没用了，所以把下一行的值覆盖到A行中，滚动计算。

在本题中，滚动数组第0行存放0 2 4 6 8…行的杨辉三角的值，滚动数组的第1行存1 3 5 7…行的杨辉三角的值。因此我们只需要将 行 % 2即可确定使用哪一行。

代码

//第一种解法
class Solution {
public:
    vector<int> getRow(int n) {
        vector<int> f(n+10);
        int k = n, t = 1;
        long long res = 1;
        for(int i = 0; i <= n;i++){
            f[i] = (int)res;
            res = res * (k--) / (t++);
        }
        vector<int> ans(n+1);
        for(int i = 0;i<=n;i++){
            ans[i] = f[i];
        }
        return ans;
    }
};
//第二种解法
class Solution {
public:
    vector<int> getRow(int n) {
        vector<vector<int>> f(2,vector<int>(n+1));//开辟两行即可
        for(int i = 0; i<= n;i++){
            f[i & 1][0] = f[i & 1][i] = 1;
            for(int j = 1; j< i;j++){
                f[i & 1][j] = f[i-1 & 1][j-1] + f[i-1 & 1][j];
            }
        }
        return f[n & 1];
    }
};