题目内容

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意，pos 仅仅是用于标识环的情况，并不会作为参数传递到函数中。请使用 O(1) 空间解决此题。

说明：不允许修改给定的链表。

示例

示例 1：

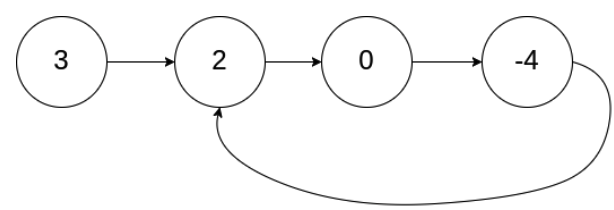
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

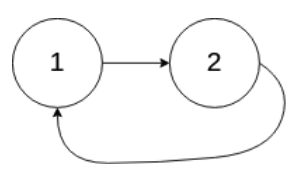
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

提示

1、链表中节点的数目范围在范围 [0, 10^4] 内
2、-10^5 <= Node.val <= 10^5
3、pos 的值为 -1 或者链表中的一个有效索引

题解

本题仍然采用双指针算法求解。思路与上一题有相似之处，有如下思考：

用两个指针i和j分别从起点开始走，i每走一步，j走两步。如果过程中j走到了null，说明链表中无环。当j继续走，与i相遇时，说明有环。这个时候，为了判断环的入口，需要让i返回起点，j在原地，然后继续往前走，当i和j第二次碰面后，碰面的节点就是环的入口。

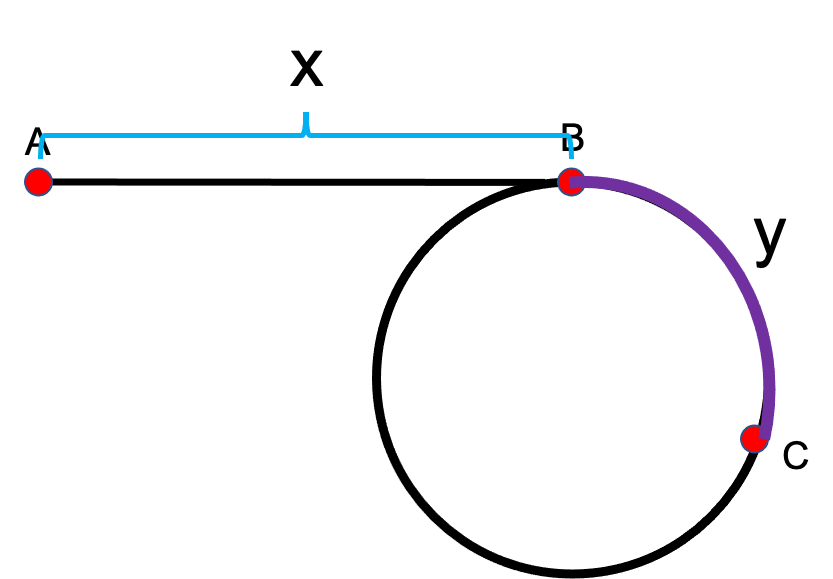
根据图，以下是证明：

A是起点，B是环的入口，C是两个指针第一次相遇点，AB之间距离为x，BC之间距离为y。当i走到B点时，由于j比i多走一倍的路程，因此j已经在环上走了x步。用z表示从C点顺时针走到B点的距离，第一次相遇j走的距离是x+(y+z)×n+y，n代表圈数，同时j走过的距离是i的两倍，也就是2(x+y)。因此就有x+(y+z)×n+y = 2(x+y)。故而求得x=(n−1)×(y+z)+z。因此，让j从C点开始走，走x步，会恰好走到B点，让 i从A点开始走，走x步，也会走到B点。

代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(!head||!head->next) return NULL;
        auto s = head,f=head->next;
        while(f){
            s = s->next,f = f->next;
            if(!f){
                return NULL;
            }
            f = f->next;
            if(s == f){
                s = head,f = f->next;
                while(s!=f){
                    s = s->next,f = f->next;
                }
                return s;
            }
        }
        return NULL;
    }  
};